[suche] hilfe

also ich muss übermorgen folgende aufgabe abgeben:



und ich steh grad total aufm schlauch, ich hab keine ahnung was ich da tun soll. wenn mir jemand helfen könnte wäre total lieb

Bei Wikipedia haste die Formel:

da setzt man die Ableitungen bzw die Funktion ein (bis zum n-ten Glied, zB von 0 bis 5 oder so)

hier kannst Du sehen, wie mit Erhöhen des Grades (degree; entspricht n in der Formel oben) die Potenzreihe immer besser zur Funktion passt (ist leider eine andere Funktion) zeichne das ganze einfach im Taschenrechner wenn Du sowas hast, dann sieht man irgendwann, für wieviele n das Ganze sinnvoll is

Dieser Beitrag wurde von schildkroet: 24 Apr 2007, 00:29 bearbeitet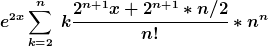

funktioniert bei mir nur ab dem zweiten glied;/
ka warum, geh aber jetzt pennen;)
morgen vllt nochmal - aber wenn wer den fehler findet, gleich sagen wo und was bitte^^
weil das erste glied fehlt isses falsch;)

a=1 und dann normal Taylor entwickeln, oder?

nee! klein a ist die stelle für die du entwickelst. x_0 sozusagen. also weglassen wenn nix gegeben is, und die differenz (x-a) bilden, wenn se gegeben is.
ausrechnen. fertig.

nunja wenn in der aufgabe x-1 steht würde ich a als 1 festlegen oder verstehe ich da was falsch?

P.S.: Dieses Applet rechnet Dir zu einer Funktion ( hier: x*EXP(2*x)) die Taylorentwicklung bis zu einem beliebigen Grad aus

hier kannst Du das Ergebnis (kopieren und einfügen) ansehen.

Die Entwicklung an der Stelle 1 ist irgendwie nicht besonders gut, bei Grad 5 (grün) ist die Näherung an die Funktion (rot) nicht besonders gut. Bei Grad 10 (blau) passts scho. Je näher man an die 0 kommt desto besser sieht das Ergebnis aus



Dieser Beitrag wurde von schildkroet: 24 Apr 2007, 11:27 bearbeitet

wahrscheinlich hast du recht. mir kam die aufgabenstellung unvollständig abgeschrieben vor und da dachte ich irgendwo steht mal ein wert für x und man soll bis zur x-1 ten potenz rechnen.

Dieser Beitrag wurde von MaxwellDemon098: 24 Apr 2007, 12:15 bearbeitet

Musste mir das auch erst ein paar mal durchlesen ^^ trotzdem ist 1 keine gute Stelle