Mathematische Knobelaufgabe Über sechs Ecken kennt man jeden auf der Welt!

ok.. ich hab den hypercube mal verallgemeinert: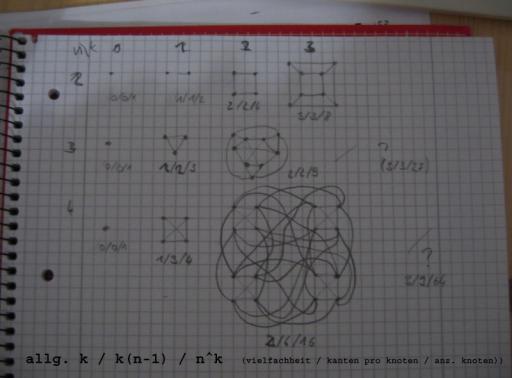


und nu rechnen wir damit:

das ist die böse variante. also 6 kanten

k = 6 d.h. der abstand zwischen 2 beliebigen knoten beträgt maximal 6 kanten im gesamten (ich such noch n namen dafür, sagen wir stth (oder ist es das, was pusti meinte))

log n (6.4mrd) = 6

n = 43.089 (zu dumm) aber 44 hoch 6 ist auch nur 7,35 mrd
(dass die ergebnisse sich ähneln ist übrigens kein zufall)

das heisst, dass k(n-1) = 6*(44-1) = 258 kanten an jedem knoten.
das heisst, jeder mensch auf der welt benötigte genau 258 freunde, damit das prinzip für jeden gilt.

für checkit: betrachte die 44 leute in einer einheit einfach als freundeskreis dummerweise müssen jeder dieser 44 215 leute aus disjunkten freundeskreisen kennen.

nehmen wir eure lasche variante:

log n (6.4mrd) = 7
n = 25.17 -> n = 26
(na guck mal einer schau, schon wieder ähnlichkeit)

k(n-1) = 7*(26-1) = 175 kanten an jedem knoten. also 175 freunde.
fine.

so und nun vernetzt mal euren baum so, dass ihr da drunter kommt. ich bin gespannt.

Des leichteren Verständnisses wegen, erklär ich meinen Gedankengang ersteinmal für den Fall, dass jeder mit jedem höchstens im 2. Grad bekannt ist, dh. über höchstens 2 Kanten (oder anders: jeder ist mit sich (0. Grad), mit seinen direkten Freunden (1. Grad) oder deren Freunden (2. Grad) bekannt).

Stellen wir uns ein 2-dimensionales Raster vor. Jeder Gitterpunkt stellt einen Menschen dar. Menschen auf einer Linie (waagerecht oder senkrecht) sind miteinander befreundet (jede Linie bildet also einen Freundeskreis). Es ist offensichtlich, dass jeder mit jedem über höchstens 2 Kanten befreundet ist. Geht man davon aus, dass das Raster durch ein Quadrat mit der Kantenlänge n begrenzt ist, wäre jeder Mensch in 2 Freundeskreisen (2 Dimensionen) und hätte demzufolge F=(n-1)*2 Freunde (Anzahl der Punkte sowohl in der Waagerechten als auch Senkrechten OHNE sich selbst). Erweitert man nun das Ganze auf d Dimensionen, wäre jeder Mensch also in d Freundeskreisen und hätte (n-1)*d Freunde. Bei M=6.4e9 Menschen und 6 Freundeskreisen ergäbe sich das viel diskutierte n^6=6.4e9, dh. eigentlich n=M^(1/6)=43.088... also n=44 => F=(44-1)*6=258, so wie schon festgestellt. Das Problem an dieser Theorie ist die Tatsache, dass das Kriterium der geringen Redundanz nicht berücksichtigt wurde, denn:

Gehen wir zurück zum 2-dimensionalen Fall: ein Mensch mit den Koordinaten (1|5) ist mit dem Menschen auf (7|2) genau über 2 andere Menschen bekannt ((1|2) und (7|5)), wobei einer ja vollkommen reichen würde. Reduzieren wir unser Quadrat nun auf ein rechtes Dreieck, fällt einer der beide weg (zB. (7|5)) und es ändert an der oben genannten Formel für F nichts, außer dass man jetzt nichtmehr sagt "JEDER Mensch hat F Freunde" sondern "ES GIBT Menschen mit maximal F Freunden (im Koordinatenursprung)" [Das kann jeder gerne selbst mit Stift und Papier nachvollziehen]. Das größere Problem ist jedoch, dass die eben "wegreduzierten" Menschen jetzt ebenfalls in diesem Dreieck untergebracht werden müssen, d.h. M ergibt sich im 2D-Fall nichtmehr durch n*n sondern in etwa durch n*n/2 (eigentlich sogar n*(n+1)/2). n wird im allgemeinen also größer sein als zuvor - ebenso F. Dafür ist auf der anderen Seite aber gewährleistet, dass es für jedes Paar Menschen nur exakt einen Weg gibt, über den sie bekannt sind, und dieser ist maximal d Kanten lang.


Es bleibt zu ermitteln, inwelcher Form die Dimension d die Abhängigkeit von n und M beeinflusst. Man muss in jeder Dimension halbieren, jedoch "halbierten" man dabei WÖRTLICH Menschen (entlang der Diagonalen)... vermutlich gilt: M=(n-1+d)!/(n-1)!/d!... viel Spaß beim Umstellen nach n... (^^,)

Macht's nicht zu kompliziert ... ;-)

Die Baumvorstellung reicht völlig ... nur das entscheidende, worauf es bei der Formel ankommt, hat noch keiner eingearbeitet

25,17?

Dieser Beitrag wurde von NEO.POP: 23 Feb 2007, 00:08 bearbeitet

Warauf kommt es dir denn an, Rene?

@Robin: einer hatte schon die richtige Idee hier gehabt ... hat nur keiner ausgebaut ;-)

@Neo: ist nen Tick zu wenig ...

Ansonsten: ich laß es noch ein zwei Tage drin, dann gibt es die Auflösung.

gib mal ne definiton von ecke...

Dieses Rätsel geht von Person X aus ... dann kann man sozusagen ein Baumdiagramm spannen. Gehe ich nun von einer beliebigen Person Y aus, die selber sich erst in der sechsen Ecke befindet, benötigt diese zu einer anderen Person Z der sechsten Ecke bis zu 12 Schritte (also Ecken), wenn beide vorher keinen gemeinsamen Bekannten haben ...

Das wäre durch aus eine weitere interessante Fragestellung ... also wenn Jeder jeden über sechs Ecken kennt ... (aber hier geht es nur um "man kennt jeden" ...) ;-)

schade, jetzt erst gelesen.. nun ist mir das problem zu trivial!

Ecke ist die Person ...

dein Freund ist die erste Ecke. Der Freund deines Freundes die zweite. Und über sechs Ecken kennt man nun jeden [d.h. nach der sechsten Ecke ist Schluß]

Wieviele ueber 6 Ecken == Eine 6/7/8er Kette?

Dieser Beitrag wurde von aktsizr: 23 Feb 2007, 06:07 bearbeitet

Es stand die These im Raum: Über sechs Ecken kennt man jeden auf der Welt.

Die daraus resultierende, interessante Frage: Wieviele Personen müßte dafür jeder kennen?

Die Frage ist unscharf formuliert. Würde ich jeden Menschen über 6 Ecken kennen, kenne ich auch jeden Menschen ohne 6 Ecken.
Eventuell paßt das Wortgefüge "in Relation stehen" besser, da man zudem noch alle Grade der Bekanntheit auf einen Nenner reduziert.

"Wie hoch ist die Anzahl der Personen in meinem privaten Interaktionshorizont, wenn ich über 6 weitere Personen mit jedem Menschen auf der Erde in Relation stehen will?"
So würde es sich nach meiner Meinung textuell begreiflicher darstellen.

es gibt wichtigere Fragen
*Gruß
~myrmi

Dieser Beitrag wurde von myrmikonos: 23 Feb 2007, 04:23 bearbeitet

"Wie hoch ist die Anzahl der Personen in meinem privaten Interaktionshorizont, wenn ich über 6 weitere Personen mit jedem Menschen auf der Erde in Relation stehen will?"
So würde es sich nach meiner Meinung textuell begreiflicher darstellen.

Nein. Mathematische Fragestellungen präzisiert man mit "genau", "nur", "maximal", "minimal", etc. und präzisen Ausdrücken.
Z.B.: Jeder Mensch steht mit jedem anderen über maximal 5 andere in Verbindung. Wie viele genau einmal vorkommende Freunde muss jede Person haben, damit er über genau 5 Personen mit 6,4 Milliarden verbunden ist. Die Knoten zählen dabei nicht zum Gesamtergebnis.

es gibt wichtigere Fragen

Da hast du allerdings Recht, zumal wir die Frage schon zur Zufriedenheit aller (bis auf Rene, stth und yocheckit) gelöst haben

Da hast du allerdings Recht, zumal wir die Frage schon zur Zufriedenheit aller (bis auf Rene, stth und yocheckit) gelöst haben

nur weil du es nicht blickst ... jeder hat gleich viele kontakte (43,9197231)

Die PISA-Studie
und ihre Ursachen !

Realschule 1960
Ein Bauer verkauft einen
Sack Kartoffeln für DM 50,-.
Die Erzeugerkosten betragen DM 40,-. Berechne den Gewinn !

Sekundarschule 1970
Ein Bauer verkauft einen
Sack Kartoffeln für DM 50,-.
Die Erzeugerkosten betragen vier Fünftel des Erlöses. Wie hoch ist der Gewinn des Bauern?
Rechenschieber nicht erlaubt!

1980 Korrektur der Formulierung (Neuauflage)
Ein/e Bauer/in verkauft eine/n
Sack/in Kartoffeln/innen einem/er Kunden/in für DM 50,-.
Die Erzeuger/innen -kosten betragen vier Fünftel/innen des Erlöses. Wie hoch ist der/die Gewinn/in des/der Bauern/in?

1990 Gymnasium
Ein Agrarökonom verkauft eine Menge subteraner Solanum tuberasum für eine Menge Geld (=G). G hat die Mächtigkeit 50. Für die Elemente aus G=g gilt g=0. Die Menge der Herstellungskosten (=H) ist um zehn Elemente weniger mächtig als die Menge G. Zeichnen Sie ein Bild der Menge H als Teilmenge G und kennzeichnen Sie die Lösungsmenge X gemäß folgender Frage: Wie mächtig ist der Gewinn.

Freie Waldorfschule 1995
Male einen Sack Kartoffeln und singe ein Lied dazu !

Integrierte Gesamtschule 1999
Ein Bauer verkauft einen Sack Kartoffeln für EUR 50,-.
Die Erzeugerkosten betragen EUR 40,-. Der Gewinn beträgt EUR 10,-. Unterstreiche das Wort „Kartoffeln“
und diskutiere mit deinen Mitschülern aus den anderen Kulturkreisen darüber.

Schule 2005 (nach der Bildungs- und Rechtschreibreform)
ein agrarinschinör fergauft ein sagg gartoffeln für 25 euro. die kosden bedragen 5 euro. der gewinn bedregt 20 euro.
aufgabe: margire den term gardoffeln und maile die lösung im pdf-format
an: klasse2a@schule.euroba

Jor 2010
sorrie, es gipt kaine gardoffeln mehr !

Die PISA-Studie
und ihre Ursachen !

Realschule 1960
Ein Bauer verkauft einen
Sack Kartoffeln für DM 50,-.
Die Erzeugerkosten betragen DM 40,-. Berechne den Gewinn !

Sekundarschule 1970
Ein Bauer verkauft einen
Sack Kartoffeln für DM 50,-.
Die Erzeugerkosten betragen vier Fünftel des Erlöses. Wie hoch ist der Gewinn des Bauern?
Rechenschieber nicht erlaubt!

1980 Korrektur der Formulierung (Neuauflage)
Ein/e Bauer/in verkauft eine/n
Sack/in Kartoffeln/innen einem/er Kunden/in für DM 50,-.
Die Erzeuger/innen -kosten betragen vier Fünftel/innen des Erlöses. Wie hoch ist der/die Gewinn/in des/der Bauern/in?

1990 Gymnasium
Ein Agrarökonom verkauft eine Menge subteraner Solanum tuberasum für eine Menge Geld (=G). G hat die Mächtigkeit 50. Für die Elemente aus G=g gilt g=0. Die Menge der Herstellungskosten (=H) ist um zehn Elemente weniger mächtig als die Menge G. Zeichnen Sie ein Bild der Menge H als Teilmenge G und kennzeichnen Sie die Lösungsmenge X gemäß folgender Frage: Wie mächtig ist der Gewinn.

Freie Waldorfschule 1995
Male einen Sack Kartoffeln und singe ein Lied dazu !

Integrierte Gesamtschule 1999
Ein Bauer verkauft einen Sack Kartoffeln für EUR 50,-.
Die Erzeugerkosten betragen EUR 40,-. Der Gewinn beträgt EUR 10,-. Unterstreiche das Wort „Kartoffeln“
und diskutiere mit deinen Mitschülern aus den anderen Kulturkreisen darüber.

Schule 2005 (nach der Bildungs- und Rechtschreibreform)
ein agrarinschinör fergauft ein sagg gartoffeln für 25 euro. die kosden bedragen 5 euro. der gewinn bedregt 20 euro.
aufgabe: margire den term gardoffeln und maile die lösung im pdf-format
an: klasse2a@schule.euroba

Jor 2010
sorrie, es gipt kaine gardoffeln mehr !