erm ja...
wie bereits erwähnt...
die richtige bedingung für BIBO-stabilität is, dass alle nullstellen einen negativen realteil haben, als links von der imaginär-achse liegen
ist für -1 ja durchaus der fall
ka, was die impulsantwort war...
laut wikipetra wars die ableitung der sprungantwort...
die sprungantwort ist 1/s * H(s)
die ableitung der sprungantwort wäre ja s * 1/s * H(s) = H(s)
bzw die rücktransformierte in den zeitbereich...
die rücktransformation geht immer über den residuensatz...
also lim[H(s) * (s-polstelle) * e^(st)] für s->polstelle
hier also konkret:
lim [H(s) * (s + 1) * e^(s*t)] für s = -1
du siehst, dass sich der nenner von H(s) mit dem (s + 1) wegkürzt
bleibt noch lim[s * e^(s*t)] wo du für s einfach -1 einsetzt...
h(t) ist also -e^(-t), wenn ich mich ned irre

das mit dem prinzipverlauf weiß ich nicht genau, aber ich vermute das wird ähnlich wie bei der Z-transformation sein...
also NS und PS in den PN-plan eintragen und dann schaun, wie groß das jw bei der NS oder PS ist...
unabhängig vom einheitskreis...die richtung zählt...
bei ner negativen reellen NS wäre jw = pi... bei einer rein imaginären pi/2 etc...
aber wie gesagt, ist nur geratensiehe paintskizze
ansonsten kannste den verlauf auch abschätzen...
s/(1+s) ist 0 für s->0 und 1 für extrem große s... also ein hochpass
den prinzipiellen kurvenverlauf vom hochpass kennste ja
Dieser Beitrag wurde von drölf: 18 Jul 2006, 21:54 bearbeitet angehängte Bilder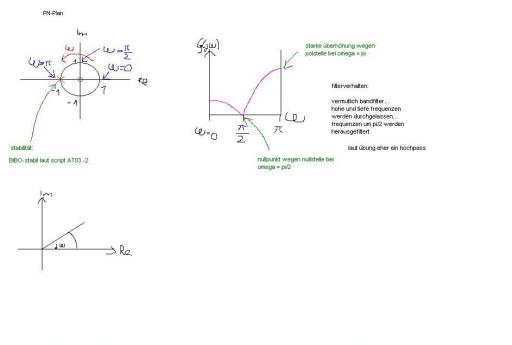
![]() ETler, ich brauche Euch! Übertragungsfunktion H(s)
ETler, ich brauche Euch! Übertragungsfunktion H(s)